Symmetric Matrix and Sparse Matrix in Hindi

Symmetric Matrix

जब कोई Matrix A व उसका Transpose Matrix A^T दोनों के सभी Data Elements समान हों तो इस प्रकार के Matrix को Symmetric Matrix कहा जाता है। यानी यदि A = A^T हो तो इस प्रकार के Matrix को Symmetric Matrix कहा जाता है। इसे हम अगले चित्र द्वारा भी समय  सकते हैं-

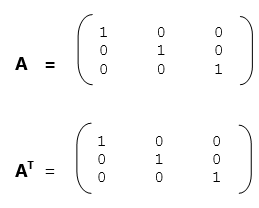
हम देख सकते हैं कि Matrix A व उसका Transpose Matrix A^T दोनों के विभिन्न Data Elements एकदम समान है, इसलिए ये एक Symmetric Matrix है।

Sparse Matrix

यदि किसी Matrix में ज्यादातर Data Elements 0 हों, तो इस प्रकार के Matrix को Sparse Matrix कहा जाता है। हालांकि ये कभी निश्चित नहीं होता है कि किस Matrix को Sparse Matrix कह सकते हैं और किसे नहीं। लेकिन फिर भी यदि किसी Matrix के कुल Data Elements में 2/3 से अधिक Elements का मान 0 हो तो इस प्रकार के Matrix को Sparse Matrix की Category में रखा जाता है। उदाहरण के लिए निम्न Matrix एक Sparse Matrix का उदाहरण है-

यदि हम इस Matrix को Memory में Store करना चाहें तो हमें कुल 9 Memory Locations के लिए Space Reserve करना होगा। जबकि हम देख सकते हैं कि इस Matrix में केवल तीन ही Data Elements उपयोगी हैं जो किसी Information को Represent कर रहे हैं। इस स्थिति में बाकी के 6 Space बेवजह Memory Space को Reserve रखेंगे।

Sparse Matrix के Data को Represent करने के लिए एक ऐसी व्‍यवस्था का प्रयोग किया जाता है जिसे 3 – Tuple Representation कहा जाता है। इस व्‍यवस्था में एक ऐसा Array Create किया जाता है जिसमें Matrix के हर मान को एक Row या Tuple के रूप में Store किया जाता है। इस Row में तीन Columns होते हैं। पहले Column में उस Non – Zero Data Element की Row का Index Number होता है। दूसरे Column में उस Non – Zero Data Element की Column का Index Number होता है और तीसरे Column में Matrix के Data Element का Actual मान होता है।

जैसे यदि उपरोक्त Matrix को ही हम Sparse Matrix के रूप में Memory में Store करना चाहें तो हम निम्नानुसार एक Array Create कर सकते हैं-

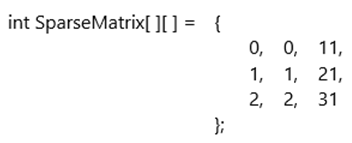
हमारे Actual Matrix में Row Number 0 व Column Number 0 पर मान 11 है। इसे एक Row या Tuple के रूप में लिखने के लिए SparseMatrix में पहले Index Number पर Row Number 0 को Fill किया गया है।

दूसरे Column में Column Number 0 को Fill किया गया है और तीसरे Column में Actual मान 11 को Fill किया गया है। यहां भी Sparse Matrix की पूरी Information को Store करने के लिए हमें 9 Memory Spaces की आवश्‍यकता होती है लेकिन यदि किसी Sparse Matrix की Size 10 * 10 की हो और उसमें केवल 20 Data Elements ऐसे हों जिन्हें 3 – Tuple में Represent करना हो तो हमें केवल 20 Locations की ही आवश्‍यकता होगी। जबकि यदि 10*10 का Matrix Create किया जाए तो हमें 100 Memory Locations की जरूरत होगी।

यानी किसी 10*10 के Sparse Matrix के केवल 20 Data को Represent करने के लिए यदि हम 3 – Tuple Representation का प्रयोग करते हैं तो हम 80 Memory Locations को बचा सकते हैं। यही Sparse Matrix का Computer Science में उपयोग है।