What is Matrix in Data Structure and how to create them?

What is Matrix in Data Structure: एक 2D Array को Industrial Area में Table कहा जाता है जबकि Scientific Area में Matrix कहते हैं। यदि किसी Company के विभिन्न Employees की Information को Manage करना हो तो हम एक 2D Array का प्रयोग करके Company के विभिन्न Employees की Information को Manage कर सकते हैं। Employees की इन Information के समूह को Table कहा जा सकता है। लेकिन जब हम Mathematical Calculations या Scientific Expressions को Handle करने के लिए एक 2D Array का प्रयोग करते हैं तो उसी 2D Array को Matrix कहा जाता है। हम विभिन्न प्रकार के Algebraic Operations को एक Array का प्रयोग करके Represent कर सकते हैं। इस Section में हम इन्ही के बारे में सीखेंगे।

Addition of Matrixes

दो Matrix का Addition तभी सम्भव है जब दोनों Matrix समान प्रकार के हों यानी दोनों Matrix के Rows व Columns की संख्‍या समान हो।

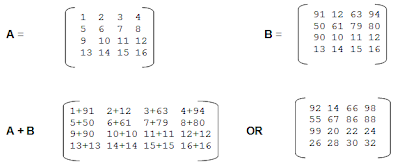
मानलो A व B दो समान प्रकार के Matrix हैं, तो Matrix A व Matrix B को एक तीसरे Matrix के रूप में Define किया जा सकता है जिसमें दोनों Matrix के सभी समान Locations का योग तीसरे Matrix में समान Location पर होता है। उदाहरण के लिए

दो Matrixes का जोड करने के लिए सबसे पहली शर्त ये है कि दोनों Matrix के Rows व Columns की संख्‍या समान हो।

जब दो Matrix जोडने लायक होते हैं तब पहले Matrix के 0,0 Location के मान को दूसरे Matrix के 0,0 Location के मान से जोड कर तीसरे Matrix के 0,0 Location पर Store किया जाता है। इसी तरह से पहले Matrix के 0,1 Location के मान को दूसरे Matrix के 0,1 Location के मान से जोडकर तीसरे Matrix के 0,1 Position पर Store करना होता है। यानी किन्ही दो Matrix को जोडने के लिए हम निम्न Algorithm का प्रयोग कर सकते हैं-

Matrix Addition Algorithm
MATRIX_ADDITION(MATRIX1, ROW1, COL1, MATRIX2, ROW2, COL2, MATRIX3, ROW3, COL3)
Here MATRIX1 is a Matrix with Size ROW1 and COL1, MATRIX2 is a Matrix with Size ROW2 and COL2, MATRIX3 is a Matrix with Size ROW3 and COL3.

1. IF ROW1 = ROW2 and COL1 = COL2 then
   PRINT “MATRIX ADDITION is Possible”
   REPEATE FOR I = 0 To M STEP SIZE 1 INCREMENT
   REPEATE FOR J = 0 To N STEP SIZE J = J + 1
   MATRIX1[I][J]=MATRIX1[I][J] + MATRIX2[I][J]
   ELSE
   PRINT “MATRIX ADDITION is not Possible”
2. EXIT

Subtraction of Matrixes

जिस तरह से हम दो Matrix को आपस में जोड सकते हैं उसी तरह से हम पहले Matrix से दूसरे Matrix को घटाकर तीसरा Matrix भी प्राप्त कर सकते हैं।

यहां ये बात ध्यान रखने वाली होती है कि यदि एक Matrix A व दूसरा Matrix B है तो A – B और B – A का परिणाम समान नहीं आता है। इसे निम्न उदाहरण से समझ सकते हैं-

किसी एक Matrix में से दूसरे Matrix को घटा कर तीसरा परिणामी Matrix प्राप्त करने के लिए भी दोनों Matrix के Rows व Columns की संख्‍या समान होना जरूरी होता है।

जब दो Matrix इस स्थिति में हों कि उन्हें घटाया जा सके तो हमें पहले Matrix की 0,0 Location के मान को दूसरे Matrix के 0,0 Location के मान में से घटा कर तीसरे Matrix के 0,0 Location पर परिणाम को Store करना होता है। ठीक इसी तरह से पहले Matrix के 0,1 Location के मान को दूसरे Matrix के 0,1 Location के मान में से घटा कर तीसरे Matrix के 0,1 Location पर परिणाम को Store करना होता है और यही प्रक्रिया हमें Matrix के अन्य सभी Locations के मानों के साथ अपनानी होती है। Matrix के Subtraction के लिए हम निम्न Algorithm का प्रयोग कर सकते हैं-

Matrix Subtraction Algorithm
MATRIX_SUBTRACTION(MATRIX1, ROW1, COL1, MATRIX2, ROW2, COL2, MATRIX3, ROW3, COL3)
Here MATRIX1 is a Matrix with Size ROW1 and COL1, MATRIX2 is a Matrix with Size ROW2 and COL2, MATRIX3 is a Matrix with Size ROW3 and COL3.

1. IF ROW1 = ROW2 and COL1 = COL2 then
   PRINT “MATRIX SUBTRACTION is Possible”
   REPEATE FOR I = 0 To M STEP SIZE I = I + 1
   REPEATE FOR J = 0 To N STEP SIZE J = J + 1
   MATRIX1[I][J]=MATRIX1[I][J] – MATRIX2[I][J]
   ELSE
   PRINT “MATRIX SUBTRACTION is not Possible”
2. EXIT